Knight's Tour Art
The following Knight's Tour reflects simplicity, beauty, and semi-symmetry in which the two left quadrants show the same path of the knight, while the two right quadrants mirror the path.
Knight's Tour Art by Dan Thomasson, July, 2001
Another interesting tour gem, a mini-Knight's Tour of only 16 moves, can be used to create the most amazing geometric pattern called a 4th dimension hypercube. Use Algebraic notation with all columns numbered from 1 to 8, bottom to top, and all rows lettered 'a' to 'h,' left to right where a1 is the bottom left square, a8 is the top left square, and h1 is the bottom right square, etc., of an 8x8 chessboard. The path of the Knight could be d8, b7, a5, b3, d2, f3, g5, f7, d6, c4, e5, c6, d4, e6, c5, e4. By placing a dot in the center of each square that the Knight moves to, then connecting each dot with a line that represents a legal Knight's move, the end result is a perfect 4th dimension hypercube. Notice that there are 16 different cubes, all of which have the same exact dimensions, inside the hypercube.
Select image to see 16 cubes within the Hypercube.
Rudi Ashdown noticed that my mini-Knight's tour of 16 moves provides only half the total moves necessary to make a complete hypercube. He has graciously provided the following completed "Knight's Tour Hypercube."
To see how a 10x10 Knight's Tour was artistically used to relieve writer's block, and to provide structure for a literary masterpiece, check out Georges Perec's 10x10 Knight's Tour.
Below you will find an interesting pattern that can be repeated over and over again to make larger and larger Open Knight's Tours. The inspiration to create this tour came from a request I received in email from Viv at the British Library. She asked: "Do you know of anywhere that shows the solution to a 9 x 9 Knight's Tour board starting in a corner square?" I could not think of a nice 9x9 tour with that specification so I created one for her.
I used Mathematica to generate all 5x5 tours that started with the first move at the bottom left corner of the board, a total of 304 tours. I selected a 5x5 tour pattern that started in the bottom left corner square and expanded it to a 9x9 tour by continuously making rotational moves of the knight around the board. I later realized that I could continue this process of making larger Open Knight's Tours. In fact, the process can continue "To Infinity & Beyond!" This phrase was made popular by Buzz Lightyear, the animated space ranger, in the movie Toy Story by Disney-Pixar in 1995.
Notice the blue letter 'S' in the center of the tour. The 'S' represents the first letter of 'Springertour,' which is the German word for 'Knight's tour.' I might incorporate this letter 'S' design as my logo for Springer Geometry. Claude Bragdon illustrates the same 'S' pattern design labeled 'Magic Lines From Euler's Squares' in his book: Projective Ornament published in 1915 by The Manas Press in Rochester, New York.
To see how a 10x10 Knight's Tour was artistically used to relieve writer's block, and to provide structure for a literary masterpiece, check out Georges Perec's 10x10 Knight's Tour.
Below you will find an interesting pattern that can be repeated over and over again to make larger and larger Open Knight's Tours. The inspiration to create this tour came from a request I received in email from Viv at the British Library. She asked: "Do you know of anywhere that shows the solution to a 9 x 9 Knight's Tour board starting in a corner square?" I could not think of a nice 9x9 tour with that specification so I created one for her.
I used Mathematica to generate all 5x5 tours that started with the first move at the bottom left corner of the board, a total of 304 tours. I selected a 5x5 tour pattern that started in the bottom left corner square and expanded it to a 9x9 tour by continuously making rotational moves of the knight around the board. I later realized that I could continue this process of making larger Open Knight's Tours. In fact, the process can continue "To Infinity & Beyond!" This phrase was made popular by Buzz Lightyear, the animated space ranger, in the movie Toy Story by Disney-Pixar in 1995.
Notice the blue letter 'S' in the center of the tour. The 'S' represents the first letter of 'Springertour,' which is the German word for 'Knight's tour.' I might incorporate this letter 'S' design as my logo for Springer Geometry. Claude Bragdon illustrates the same 'S' pattern design labeled 'Magic Lines From Euler's Squares' in his book: Projective Ornament published in 1915 by The Manas Press in Rochester, New York.
Select image to see another infinite open Knight's Tour with blue lines. - by Dan Thomasson, August 3, 2003
The same first 80 moves of the Infinite Open Knight's Tour with blue lines were also created by Johannes (Hans) Secelle and Albrecht Heeffer on March 09, 2002, to demonstrate an infinite positive integer sequence. Their sequence of moves is posted in OEIS.org, Part 55 of the On-Line Encyclopedia of Integer Sequences under the A068614 section and my archived site, Knight' Tour Art, under A068608.
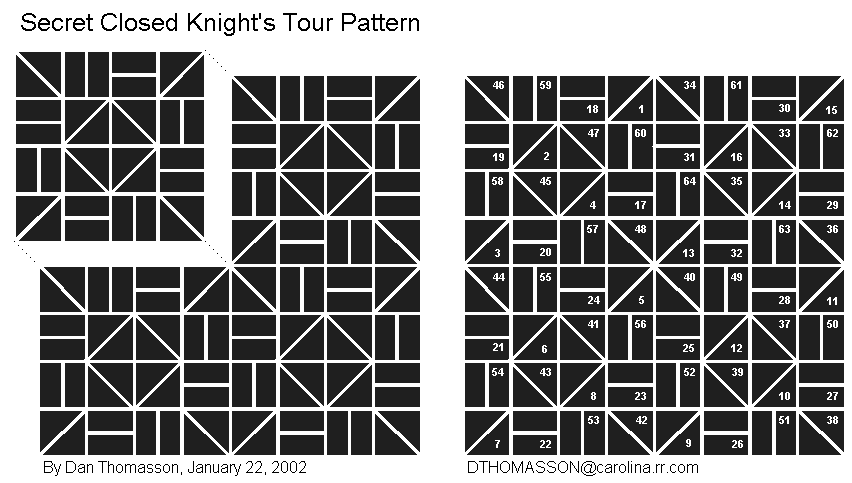
Below you will find another interesting pattern that can be repeated over and over again to make larger and larger Closed Knight's Tours. The pattern comes from my Closed Knight's Tour Solution Key. Ceramic tiles, wood, or plastic can be cut into these basic shapes to make the secret closed knight's tour pattern. The cut pieces could then be put on floors, walls, or tabletops. For simplicity, create the pattern for an 8x8 square board. Do not put numbers on the top of the pieces. If you want to make it into a puzzle, cut out the pieces and put the corresponding numbers on the back of the pieces in a very light shade or impression.
When I practice creating Knight's Tours on paper with checkerboard squares, I can quickly complete an 8x8 square closed Knight's Tour in 15 seconds by marking off each Knight move on the squares with the following symbols: /, -, \, |. I first use '/' for all diamond shape patterns leaning in the same direction as '/' in all four quadrants. I then use '-' for square shape patterns in all four quadrants, then '\' for the opposite diamond patterns, and finally '|' for the opposite square patterns.
After doing hundreds, possibly thousands of Knight's Tours, using those four simple marks (which by the way are much easier to jot down with a pencil than numbers - especially if the tour is 10,816 squares), I realized that they made a neat pattern on the chessboard which could be reproduced with tiles. I just follow the path pattern that I use for the Closed Knight's Tour Solution Key and other tours that are displayed on the Knight's Tour web page.
I might consider making a cool poster out of it or some of the other tours I've created. There is a definite symmetrical pattern. Just think, by creating that one quadrant, it can be used as computer wallpaper, web-page background, watermarks, or quilts by tiling it. Experiment by changing the line color and thickness, and the tile color. By combining these four shapes in various ways, alphabets, number systems, and ciphers can be easily created. Who knows, maybe there could be a fictional story written that centers its plot around the patterns in the Secret Closed Knight's Tour.
Below you will find another interesting pattern that can be repeated over and over again to make larger and larger Closed Knight's Tours. The pattern comes from my Closed Knight's Tour Solution Key. Ceramic tiles, wood, or plastic can be cut into these basic shapes to make the secret closed knight's tour pattern. The cut pieces could then be put on floors, walls, or tabletops. For simplicity, create the pattern for an 8x8 square board. Do not put numbers on the top of the pieces. If you want to make it into a puzzle, cut out the pieces and put the corresponding numbers on the back of the pieces in a very light shade or impression.
When I practice creating Knight's Tours on paper with checkerboard squares, I can quickly complete an 8x8 square closed Knight's Tour in 15 seconds by marking off each Knight move on the squares with the following symbols: /, -, \, |. I first use '/' for all diamond shape patterns leaning in the same direction as '/' in all four quadrants. I then use '-' for square shape patterns in all four quadrants, then '\' for the opposite diamond patterns, and finally '|' for the opposite square patterns.
After doing hundreds, possibly thousands of Knight's Tours, using those four simple marks (which by the way are much easier to jot down with a pencil than numbers - especially if the tour is 10,816 squares), I realized that they made a neat pattern on the chessboard which could be reproduced with tiles. I just follow the path pattern that I use for the Closed Knight's Tour Solution Key and other tours that are displayed on the Knight's Tour web page.
I might consider making a cool poster out of it or some of the other tours I've created. There is a definite symmetrical pattern. Just think, by creating that one quadrant, it can be used as computer wallpaper, web-page background, watermarks, or quilts by tiling it. Experiment by changing the line color and thickness, and the tile color. By combining these four shapes in various ways, alphabets, number systems, and ciphers can be easily created. Who knows, maybe there could be a fictional story written that centers its plot around the patterns in the Secret Closed Knight's Tour.
8x8 Secret Closed Knight's Tour Patterm - Dan Thomasson, January 22, 2002
See Knight's Tour Tessellations for information about how the following Astersphaira (Star Sphere) was conceived.
Astersphaira (Star Sphere) by Dan Thomasson/Paul Bourke June 2002
Look at the following excellent 3-d artwork by Jason Martineau. His Zonohedron encompasses all of the patterns (square, diamond, and rhombus) made by the moves of the Knight on the chessboard.
Zonohedron by Jason Martineau
The following Closed Knight's Tour shows how Knight's Tours can contain tessellation patterns. This same tour also contains a pattern that if animated could be called a pinwheel, windmill, water mill, fan or whatever you might think it resembles. Look closely at other Knight's Tours to see what familiar patterns you can find.
8x8 Knight's Tour Pinwheel - by Dan Thomasson, July 2002
A gentleman by the name of Biniam Gebremichael has made very nice 64x64 color gradient Knight's Tours.
64x64 Color Gradient Knight's Tour-1
64x64 Color Gradient Knight's Tour-2
In the above Knight's Tour-1, the Knight starts at square (0,1) - top left corner, second column, and first row from top to bottom. Using a Warnsdorf heuristic algorithm, the Knight moves around the board visiting all squares. A gradient color pattern fills the board with the first few squares being black, then dark green, then finally light green for the last few moves. The last square visited is (63,1) colored red (enlarge the image for a better view). Different designs can be obtained by varying the colors, the generation formulas, or the starting square of the Knight, as seen above in Knight's Tour-2.
I've finally decided to let computers solve additional Knight's Tours. There are many algorithms already published that can solve Knight's Tours such as the Warnsdorf algorithm previously mentioned. The algorithm I like best is from Dr. Colin Rose. Michael Taktikos, a Germán mathematician, and I have modified the code to include an end list so that both the first few moves, and last few moves can be chosen to solve specific types of tours (especially closed tours).
For now, please take a look at some unique 3x10 Closed Knight's Tours and (3x4, 3x7), 3x9, and 5x5 symmetrically Open Knight's Tours generated by my PC using Dr. Colin Rose's Mathematica code. Mathematica has also solved all 9,862 uniquely Closed Knight's Tours of a 6x6 square board. Here are the first 10 of 168! / (63! *(168-63)!), just slightly less than 1 octillion (10^27) U.S.A and 10^48 in Great Britain, 8x8 sequentially backtracked Knight's Tours. Here are some nice 10x10 90-degree rotational quaternary symmetric tours.
Juro Bystricky from Canada was trying to calculate all 8x8 Knight's Tours on his computer. He wrote a program that printed out all tours in a text format. After a few months, precisely 1973 hours, he had to stop calculating new Knight's Tour solutions. There were simply too many viruses that required applying service packs, and he finally had to reboot the machine which terminated the program. The program itself ran as an idle task on a 2.4G Pentium 4 machine. It calculated over 18 Million solutions that were logged into a 4GB size text file. Since he found no tool that can actually handle text files of this size, Juro split the file into chunks of 100,000 solutions each. He then zipped the file chunks, compressing them into about a 400 MB file that would easily fit onto a single CD.
I've finally decided to let computers solve additional Knight's Tours. There are many algorithms already published that can solve Knight's Tours such as the Warnsdorf algorithm previously mentioned. The algorithm I like best is from Dr. Colin Rose. Michael Taktikos, a Germán mathematician, and I have modified the code to include an end list so that both the first few moves, and last few moves can be chosen to solve specific types of tours (especially closed tours).
For now, please take a look at some unique 3x10 Closed Knight's Tours and (3x4, 3x7), 3x9, and 5x5 symmetrically Open Knight's Tours generated by my PC using Dr. Colin Rose's Mathematica code. Mathematica has also solved all 9,862 uniquely Closed Knight's Tours of a 6x6 square board. Here are the first 10 of 168! / (63! *(168-63)!), just slightly less than 1 octillion (10^27) U.S.A and 10^48 in Great Britain, 8x8 sequentially backtracked Knight's Tours. Here are some nice 10x10 90-degree rotational quaternary symmetric tours.
Juro Bystricky from Canada was trying to calculate all 8x8 Knight's Tours on his computer. He wrote a program that printed out all tours in a text format. After a few months, precisely 1973 hours, he had to stop calculating new Knight's Tour solutions. There were simply too many viruses that required applying service packs, and he finally had to reboot the machine which terminated the program. The program itself ran as an idle task on a 2.4G Pentium 4 machine. It calculated over 18 Million solutions that were logged into a 4GB size text file. Since he found no tool that can actually handle text files of this size, Juro split the file into chunks of 100,000 solutions each. He then zipped the file chunks, compressing them into about a 400 MB file that would easily fit onto a single CD.