Knight Moves Derived from Dice
Knight moves derived from dice can be used to create perspective drawing charts, designing polygons and polyhedrons, DNA analysis, calendars, clocks, factoring charts, displaying the moves of the Knight on a chessboard, and a myriad of other things.
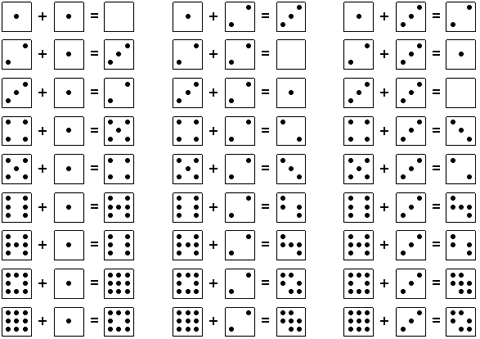
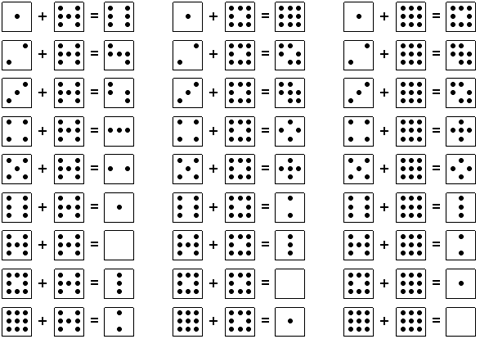
The following figures show dice numbered from 1 to 9. By using these dice, I developed a new type of number sequence matrix. When adding the dice together, I cancel out any dots that overlap the same position and add any dots that do not overlap. Therefore, 2 + 2 = 0 because the 2 dots on each dice overlap each other, and 4 + 2 = 2 because 2 dots overlap canceling out 2 dots and leaving 2 dots.
The following figures show dice numbered from 1 to 9. By using these dice, I developed a new type of number sequence matrix. When adding the dice together, I cancel out any dots that overlap the same position and add any dots that do not overlap. Therefore, 2 + 2 = 0 because the 2 dots on each dice overlap each other, and 4 + 2 = 2 because 2 dots overlap canceling out 2 dots and leaving 2 dots.
Dice 1-3 of 9
Dice 4-6 of 9
Dice 7-9 of 9
A 9x9 matrix created from the three previous charts.
Dice dots converted to actual numbers.
Circled all number pairs that have a one number difference.
Circled all number sequences of 4 consecutive numbers.
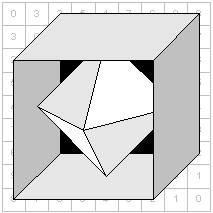
Even with the following small matrix examples, simple polygons and polyhedrons can be created.
Can you see the two octahedrons in the above figure?
3d Diamond (Octahedron) in a box.
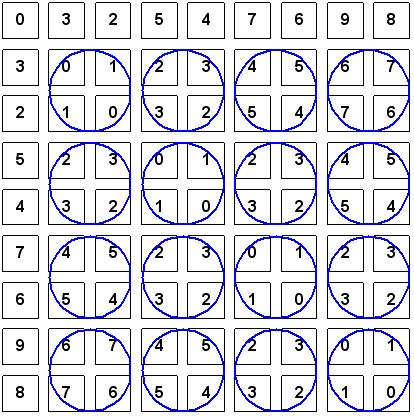
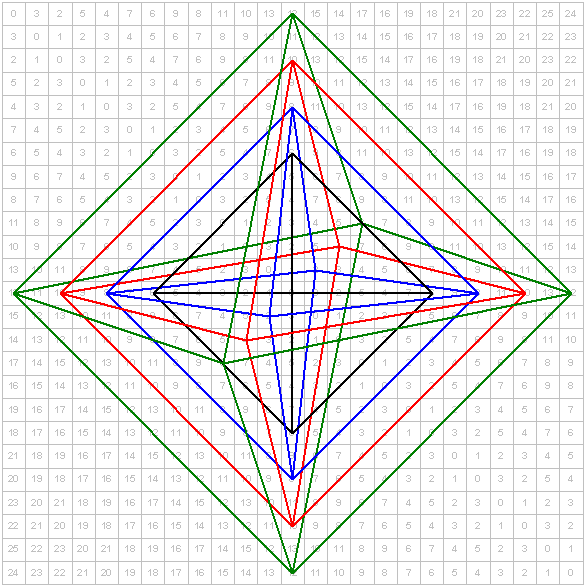
The 9x9 matrix created by dice numbers has a hidden pattern that can be tessellated. Simply connect all two or more like numbers that reside next to each other with dark straight lines. Check out the following results.
I use blue lines to connect even numbers and red lines to connect odd numbers.
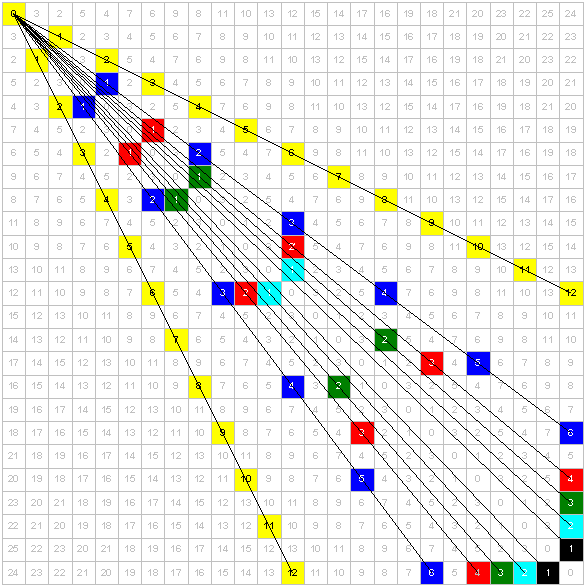
I decided to create a larger chart by using dice numbered from 1 to 25. I applied the same technique for adding dice together and canceling out matching dots to derive at new number sequences.
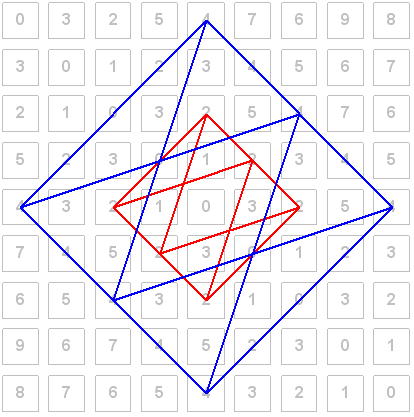
The following chart can be used as a factoring chart (notice the factors of number 12). It can also be used as a perspective drawing chart. For now, look at the squares highlighted in yellow where you will notice that they have the same spacing as the Knight's moves on the chessboard. Also, the angle in degrees from one yellow square to the next is 26.565. Check out KT Primes to learn about the significance of the degrees made by Knight's moves.
12 Knight's Moves Factoring Chart
Here is an example of how to use the matrix for drawing polyhedrons in perspective.
This figure shows the growth of an octahedron.