KT Latin Squares III

Knight's Tour Latin Squares III

KT Latin Square - © Dan Thomasson, 11-14-2005

Check out the Knight's Tour Tessellation Construction I page that shows how to make a single knight's tour circuit out of the same four mini-knight's tours shown above.

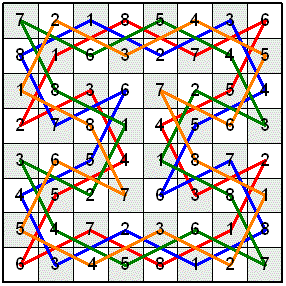
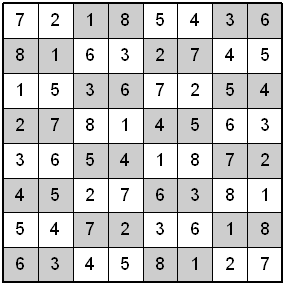
In the Knight's Tour Latin Square shown above, only one instance of each integer from 1 to 8 is in each row and column. The following four 16-Move Mini-Knight's Tours were combined to make the Latin Square. The Knight's moves for each tour are numbered from 1 to 8, then 1 to 8 repeatedly to complete the tour. Check out the following mini-knight's tours.

Knight's Tour-1

Knight's Tour-2

Knight's Tour-3

Knight's Tour-4

After filling in the four tours shown above with the same color as their line color, they can be combined into one piece that can be tessellated.

Knight's Tour Latin Square Tessellation

Knight's Tour Latin Square Tessellation Art

There are all sorts of fun math oddities that can be found within this Knight's Tour Latin Square. Notice in the diagram below on the left that each alternating horizontal number pair adds up to 9. Also, if you take the alternating horizontal number pairs as one number each (i.e. 7 and 2 as 72), they are multiples of 9 (i.e. 72 is 9x8).

Latin Square-1

Latin Square-2

Alternating groups of 4 numbers each are shown in the above Latin Square on the right. Consider each group of 4 numbers as one number (i.e. 7, 2, 1, 8 as 7218). Divide 7218 by 9 to get 802. Do the same thing to all the 4-digit numbers on the left half of the square. Add up these 8 numbers to get 4444. Now do the same thing to the right half of the square. Notice that they also add up to 4444.

7218 / 9 = 802    5436 / 9 = 604
8163 / 9 = 907    2745 / 9 = 305
1836 / 9 = 204    7254 / 9 = 806
2781 / 9 = 309    4563 / 9 = 507
3654 / 9 = 406    1872 / 9 = 208
4527 / 9 = 503    6381 / 9 = 709
5472 / 9 = 608    3618 / 9 = 402
6345 / 9 = 705    8127 / 9 = 903
4444 4444

When all the numbers are divided by 9, the results are 3-digit numbers with a zero in the middle. Also, the digits on either side of the zero for the first eight 3-digit results on the left side of the board, contain each of the digits from 2-9. The same occurs for the 3-digit results on the right side of the board.

I found it interesting that 4444 is also the exact number of solutions to the excellent "Calmplex puzzle" designed by Andrew Snowie in Canada.

Look at the results when doing the same dividing/adding process for each entire row:

72185436 / 9 = 8020604
81632745 / 9 = 9070305
18367254 / 9 = 2040806
27814563 / 9 = 3090507
36541872 / 9 = 4060208
45276381 / 9 = 5030709
54723618 / 9 = 6080402
63458127 / 9 = 7050903
44444444

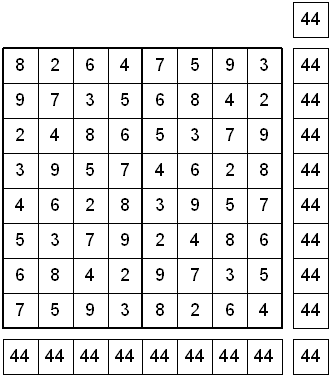
Let's see how we can make a new 8x8 Magic Latin Square from the previous eight 8-digit results. All the rows, columns, and main diagonals should each add up to 44.

1. Remove all the zeros in each number to get the following eight 4-digit numbers.

8264
9735
2486
3957
4628
5379
6842
7593

2. Place these eight 4-digit numbers down the left side of an 8x8 grid square as shown in the square below.

Magic Latin Square

3. Reverse the order (vertically flip) of the eight 4-digit numbers and place them down the right side of the same square as shown above.
4. Add up all the rows, columns, and main diagonals to get 44 for each one.
5. Subtract "1" from all the digits inside the square to get a new Magic Constant of 36.

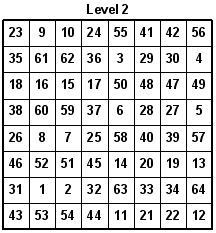
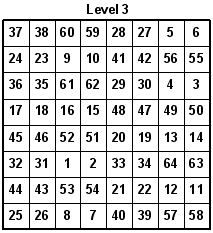
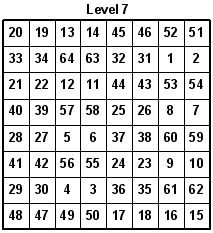
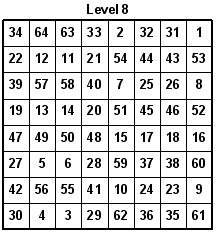
With the new 8x8 Magic Latin Square, we can make an 8x8x8 Magic Latin Cube where even the main diagonals of all faces of the cube, and the major internal diagonals equals 44. Also, all rows, columns, and pillars equal 44. Look at the eight levels. One row is rotated up each time to create a new level.

Magic Latin Cube-L1

Magic Latin Cube-L2

Magic Latin Cube-L3

Magic Latin Cube-L4

Magic Latin Cube-L5

Magic Latin Cube-L6

Magic Latin Cube-L7

Magic Latin Cube-L8

There are several number groups based on the number 9, or multiples of 9, that can be found in the original Knight's Tour Latin Square. Here are a couple groups. See what other groups you can find.

Here is another Latin Cube I designed that is based on a Magic Square originating from 3-d Knight Moves. All rows, columns, main diagonals, and pillars each add up to 260.

Latin Cube-L1

Latin Cube-L2

Latin Cube-L3

Latin Cube-L4

Latin Cube-L5

Latin Cube-L6

Latin Cube-L7

Latin Cube-L8

I'd like to thank Guenter Stertenbrink for indirectly giving me the idea to create Knight's Tour Latin Squares when he mentioned he was interested in working on Sudoku Knight's Tour problems. Latin Squares and Sudoku problems are very similar in their construction, but I find the constraints of the 3x3 squares in Sudoku problems to be a bit of an issue when creating Knight tours. I did, however, design an Order 36 Sudoku based on a 6x6 closed Knight's Tour.